בחשכת הלילה
Member
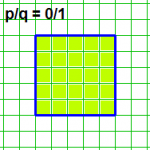
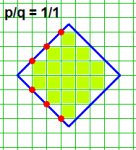
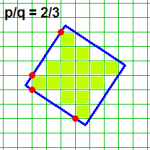
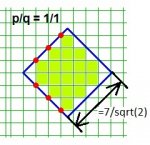
בתמונה המצורפת משורטט פולימינו ש"רוחבו" שווה 18 משבצות, וגם "גובהו שווה 18 משבצות, והוא כלוא בריבוע שצלעו שווה 14 משבצות.
שאלה: מהו ה"גובה" (ה"רוחב") המקסימלי של פולימינו הכלוא בריבוע שצלעו שווה n משבצות?
יש השערה, שהתשובה היא [n*sqrt(2)-1]. האם מישהו יכול להוכיח את ההשערה, או להציג נוסחה "יותר נכונה"?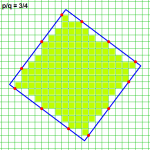
שאלה: מהו ה"גובה" (ה"רוחב") המקסימלי של פולימינו הכלוא בריבוע שצלעו שווה n משבצות?
יש השערה, שהתשובה היא [n*sqrt(2)-1]. האם מישהו יכול להוכיח את ההשערה, או להציג נוסחה "יותר נכונה"?