בחשכת הלילה
Member
אתר חידות פופולרי ברוסית. רוב החידות קלילות, או ניתנות לחישוב מהיר במחשב. למשל: מיצאו מספר תלת-ספרתי בעל תכונה מסוימת. אפשר להריץ תכנית פשוטה שתרוץ על כל המספרים התלת-ספרתיים ולבדוק אם מתקיימת בהם אותה תכונה. מה גם שבדר"כ די להקליד את התשובה הסופית, בלי צורך לפרט את דרך מציאת הפתרון.
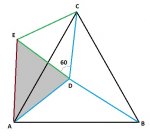
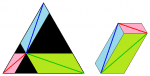
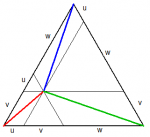
עם זאת, מפעם לפעם מופיעות בו גם בעיות מעניינות, ברמת קושי זו או אחרת, ולפעמים נדרש פתרון מפורט.
עם זאת, מפעם לפעם מופיעות בו גם בעיות מעניינות, ברמת קושי זו או אחרת, ולפעמים נדרש פתרון מפורט.